在层峦叠嶂的山区修建高速公路，测量工程师们常被一个经典的“精度悖论”所困扰：线路绵延数十公里，地形起伏超千米，如何能让一张庞大的设计图纸，在全局和局部都保持厘米级、毫米级的精准？

传统的单一坐标系或简单的分段方法，在剧烈的投影变形面前显得力不从心。我公司在西部某复杂山区高速公路项目中的测量实践，通过构建 “坐标系联邦”与“控制网挂靠” 的精密工程控制体系，成功攻克了这一难题。

一、困局：统一精度与剧烈地形的正面冲突

核心冲突点在于“投影变形”。在广袤的山区，若强制使用一套坐标系，会导致图纸上的尺寸与实地尺寸因投影变形而产生显著差异。规范要求此项变形必须小于2.5厘米/公里，对于特长隧道、特大桥等关键工程，要求更是严苛至1厘米/公里。

这带来了一个两难抉择：

若全局统一：无法满足局部精度，危及工程质量和安全。

若简单切分：设计图纸无法无缝对接，犹如“拼图错误”，极大影响设计效率和施工协同。

项目目标非常明确：必须在“一张图”的设计框架下，实现从全局到局部的全链条精度控制。 整个技术方案的完整流程如下：

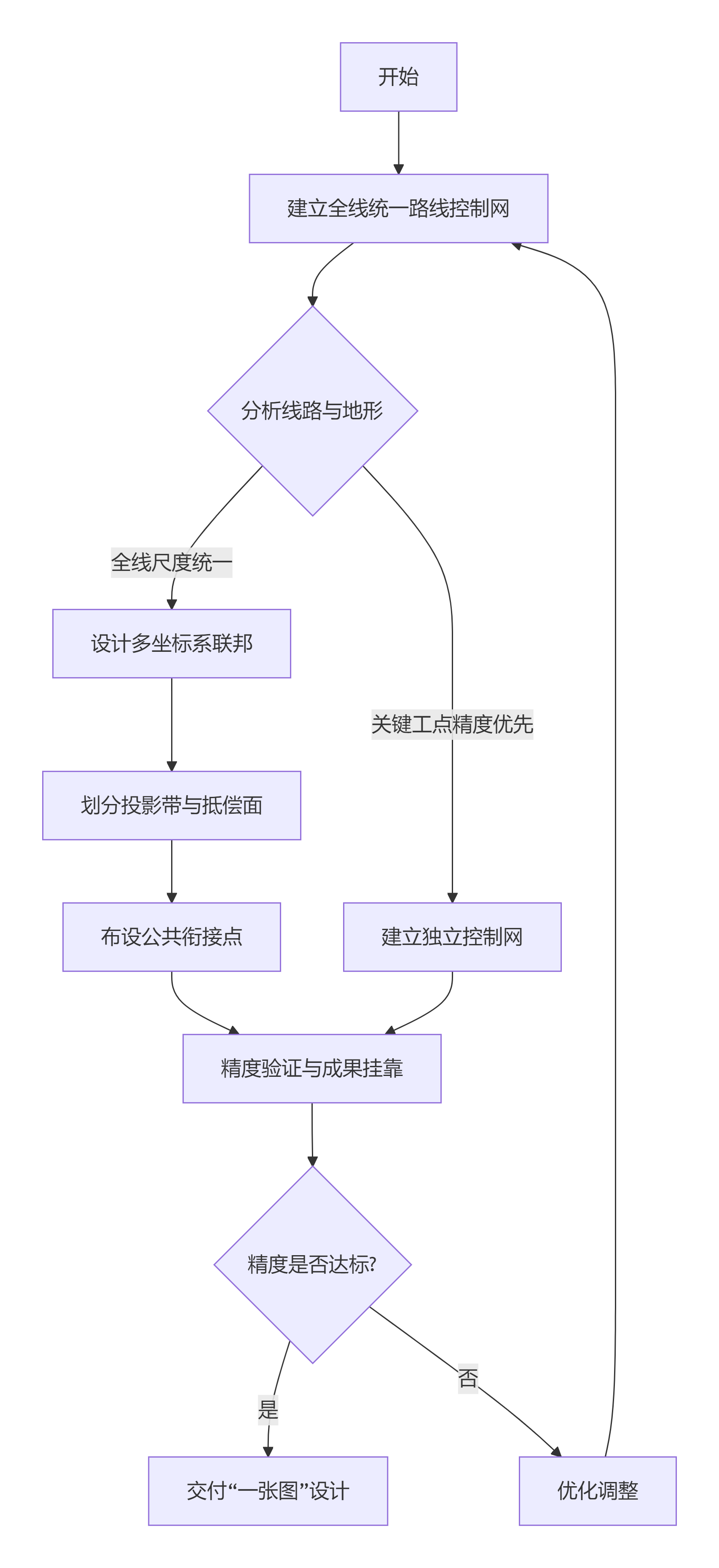
二、破局：构建“坐标系联邦”，实现全局无缝衔接

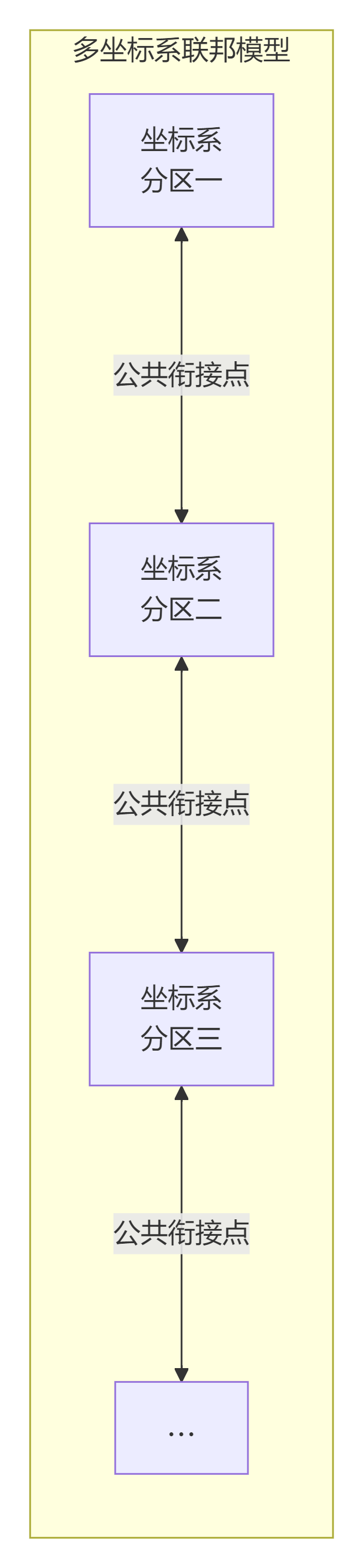
项目团队的核心创新在于，提出了 “分区抵偿、公共点衔接” 的“坐标系联邦”模型。这不是简单的切割，而是构建了一个精密的、内部高度协同的系统。

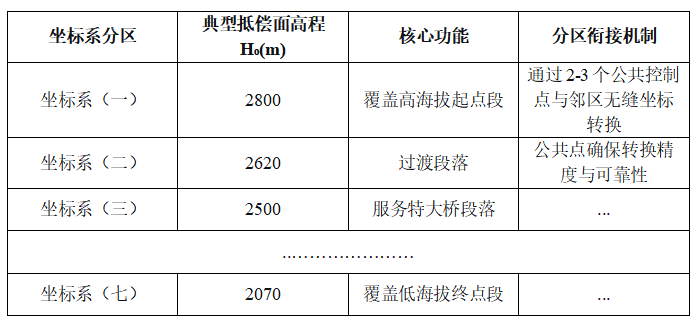
1. 统一基准下的“柔性”分区：

所有分区坐标系均基于国家大地坐标系椭球，并采用统一的中央子午线。关键在于，为每个地形起伏特征相近的段落，动态地计算并设定一个最佳的 “抵偿高程面”。

技术核心：抵偿面选择公式
投影变形主要来自两部分，其计算公式可简化为：
ΔS = S * [ (Yₘ² / 2R²) - (H - H₀) / R ]
其中，ΔS为长度变形值，S为实地边长，Yₘ为距中央子午线距离，R为地球半径，H为点的高程，H₀即为抵偿面高程。

通过精确计算并为每个分区选定最优的 H₀，我们能够有效“抵消”变形，将 ΔS 控制在规范允许的范围内。

这一“联邦”系统的运作机制，确保了宏观尺度上的统一性，其协同模式如下图所示：

2. 如何实现“一张图”设计？

在这一体系下，设计人员无需关心后台复杂的坐标转换。真正实现了 “微观精密绘图，宏观无缝成图”。

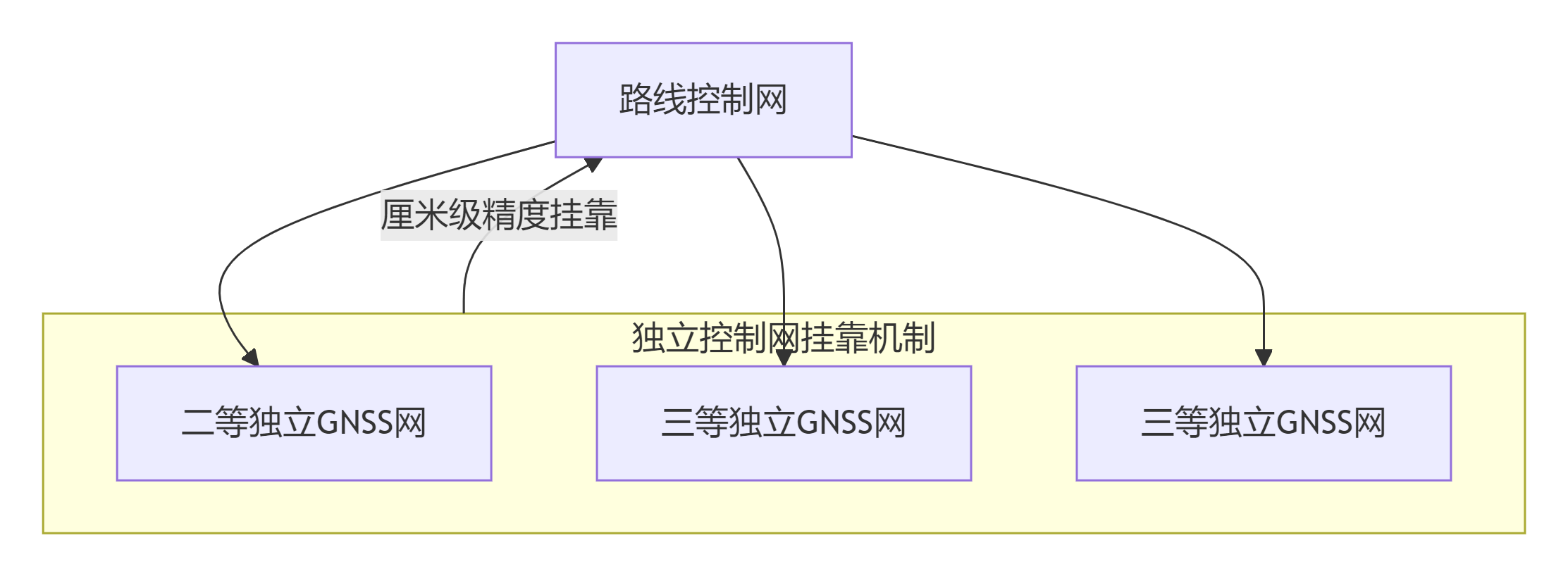
三、攻坚：关键工程的“精度特区”与全局挂靠

   对于决定线路走向的特大构造物，我们在统一的“联邦”体系下，设立了精度更高的 “特别控制区” ，即独立控制网。其与整体路线控制网的关系如下：

1. 特长隧道的“相对精度优先”策略：

在某超长隧道（长约6.6公里，进出口高差超200米）项目中，团队面临一个极端情况：理论上已无法找到一组参数使所有点位均满足1cm/km的极限要求。

解决方案如下：

确保生命线精度：果断放弃不切实际的“全点达标”，采用 “一点一方向” 法建立高等独立网。该方法的精髓在于，优先保障隧道进出口关键控制点之间的相对精度（优于1/10万），这是隧道精准贯通的“生命线”。

智慧妥协与全局融合：在承认洞口路基段存在稍大（1.8cm/km）投影变形的同时，通过严密的数学处理，确保独立网成果能平滑挂靠回路线控制网，位移较差被严格控制在厘米级，实现了“内部超高精度”与“外部顺畅衔接”的完美统一。

2. 特大桥与隧道的“标准自治”模式：

   对于其他特大桥梁和隧道，项目则成功采用 “两点固定”法，使其独立控制网内所有点的投影变形值全部小于1cm/km，内部相对精度远高于规范要求，并同样实现了与路线控制网的厘米级完美挂靠。

四、结论：一套可复用的复杂线性工程测量方法论

这项成功的实践，其价值远超单个项目。它系统地回答了一个经典难题：如何在宏观的统一性与微观的精确性之间找到最优解。

“坐标系联邦”模型，解决了大高差长线路的投影变形难题，是保障设计整体性的基石。

“控制网挂靠”机制，实现了关键工点局部精度的极限突破，是保障工程安全性的关键。

这套体系形成了一套完整的方法论，为未来穿越崇山峻岭的铁路、公路、输水渠道等重大线性工程，提供了经过实战检验的、可靠的精密测量系统解决方案，具有极高的推广和借鉴价值。